Object detection is one important type of computer vision task: given an image, localize and identify the relevant objects in it.
Photo by Ancaro Project on Unsplash
Object detection algorithms can solve problems difficult for humans, like identifying vehicle models from satellite images, counting the number of people in a crowd, or rejecting unripe fruits from a conveyor belt of fresh produce. The last example is what’s known as a sporadic visual search problem, where a huge stream of repetitive data contains anomalies only infrequently and sporadically. Humans struggle with these types of problems due to cognitive fatigue. Object detection algorithms, however, excel at this.
A perfect example of the sporadic visual search problem is X-ray baggage screening at museums. At the entrance to a museum, security operators may scan passengers’ bags with X-ray machines to detect threats like knives or handguns. Baggage screeners see thousands of bags a day, but still need to identify the single bag that contains a threat.
An X-ray scanner at the entrance to the Louvre museum.
At Synapse Technology, we use an object detection model to tackle this problem. A model in this context is an algorithm trained on a large number of labeled examples to solve a task. Let’s train an object detection model, then run it against each X-ray image the bag screener inspects.
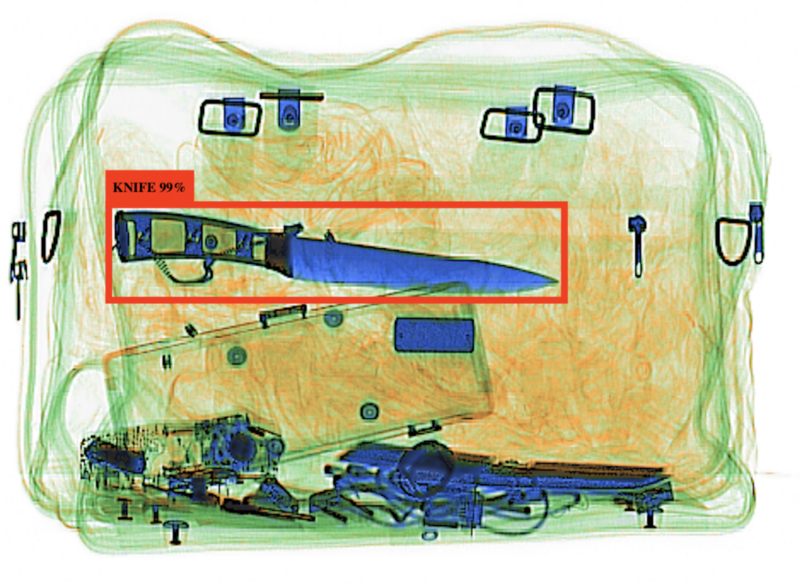A straightforward example: the knife stands out in this bag.
Detection can get much more difficult, though, depending on the bag contents and arrangement.
This bag contains a knife. Can you spot it?
It’s hard to tell whether this bag contains a threat, even with a very good object detection model. That’s why we use multiple models in ensemble to do our detections. If two models both detect the same object, there’s a much higher chance that something is actually there. Using multiple models can also improve detection rate and lower false alarms by making the whole system more robust towards uncertain/difficult cases. Ensemble detection also allows us to compare different model architectures against each other to continuously improve our product. Finally, it allows us to scale the number of threat classes we support: each model supports some set of threats, and ensemble detection makes it easy to incorporate a new model’s set of threats into the ensemble.
Implementing ensemble detection presents additional challenges beyond single object detection. Here, I’ll describe how we approached these challenges.
How can a multi-model ensemble be better than a single model?
Suppose we have two object detection models, Model A and Model B. Each of them has detected some objects in the image, and each detection has an associated confidence score.
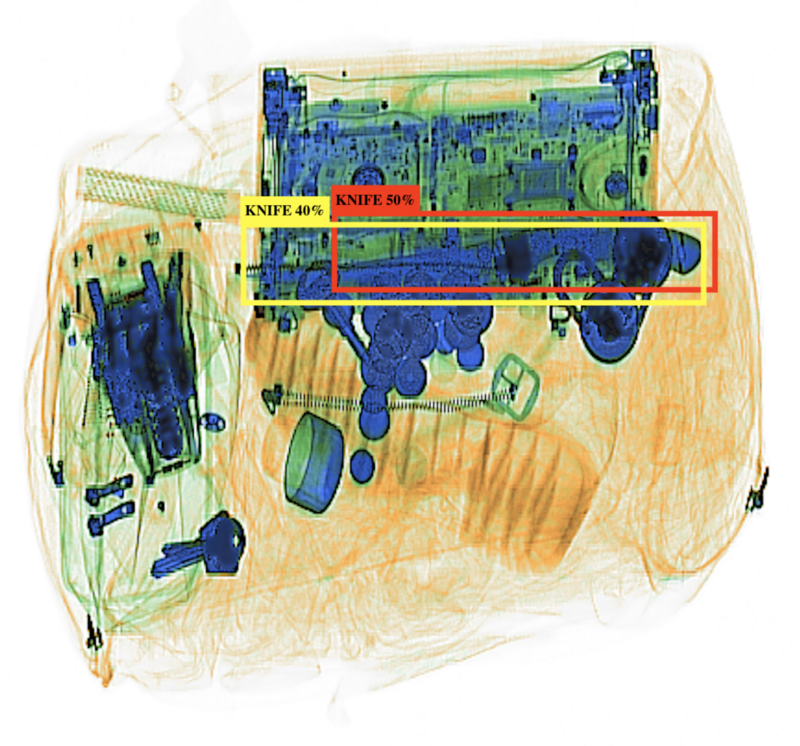The two different models have detected a threat. Note that is the same image as the previous one.
Model A (red) and Model B (yellow) have both detected a knife in the top right corner of the image, but neither model has a high enough confidence score alone for us to conclude that there is a threat in the image. If we consider the models as an ensemble, though, we observe that since two of their detections overlap, they probably refer to the same object. Given that they refer to the same object, there is a much greater probability that something is actually there. For example, if the confidence scores are the probability that each detection is a true positive (rather than a false positive), then the probability that the ensemble is a true detection is 0.7, which is greater than either detection alone (see calculations below).
prob_threat_modelA = 0.4
prob_threat_modelB = 0.5
prob_nonthreat_ensemble = (1 - prob_threat_modelA) * (1 - prob_threat_modelB)
# = (1 - 0.4) * (1 - 0.5)
# = 0.6 * 0.5
# prob_nonthreat_ensemble = 0.3
prob_threat_ensemble = (1 - prob_nonthreat_ensemble)
# = 1 - 0.3
# prob_threat_ensemble = 0.7
Ensemble detection can improve the outcome of this example, but also even more complex examples. Let’s formalize the problem and address further extensions.
Input: For a single image, each detection model independently returns a set of inferences, which are composed of a bounding box, a label, and a confidence score. The detection model will only generate one inference for each object it thinks is in the image. In the image above, Model A has returned one inference and Model B has returned one inference. Model A’s inference has the label “knife” and a confidence score of 40%, meaning that it’s 40% sure that the inference is correct.
Output: After ensemble detection, return a list of inferences, one per perceived threat in the image (no disagreements or redundancies). These inferences must have high confidence scores.
How can you implement multi-model ensemble voting for object detection?
Let’s consider a hypothetical example with the same two models, but more inferences:
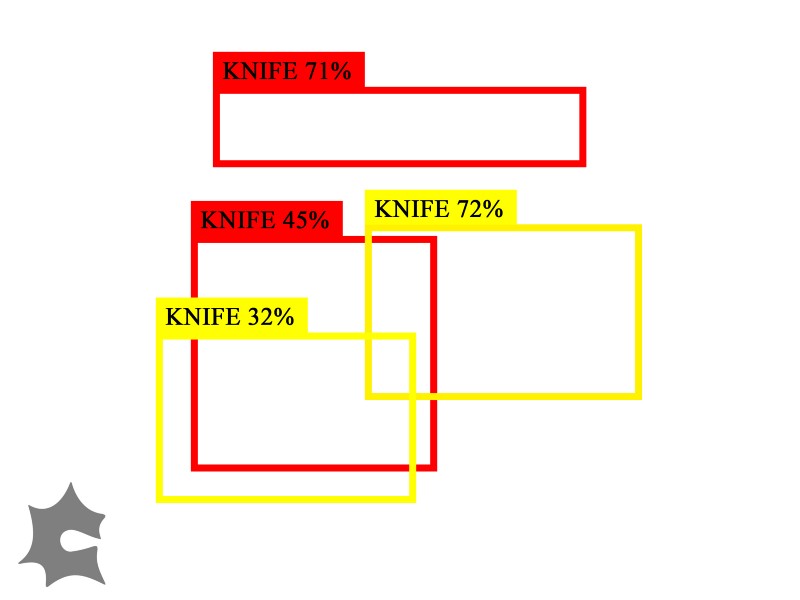Model A and Model B have detected more objects in this hypothetical image. Some of these perceived objects overlap.
In this case, we can’t just group overlapping inferences as one “ground truth object” like in the first example because two of Model B’s inferences overlap. Model B thinks that there are two different overlapping objects in the lower half of the image, but Model A thinks that there is one. How do we group them? What if there were even more inferences than this? Let’s model this as a graph problem.
Graph model for inference cliques
Create a vertex for each inference. Let the vertex’s color indicate the model it came from (e.g. red for Model A, yellow for Model B). Draw an edge between two inferences if their bounding boxes overlap. Weight this edge by how much they overlap, in particular, their intersection over union (IoU) score.
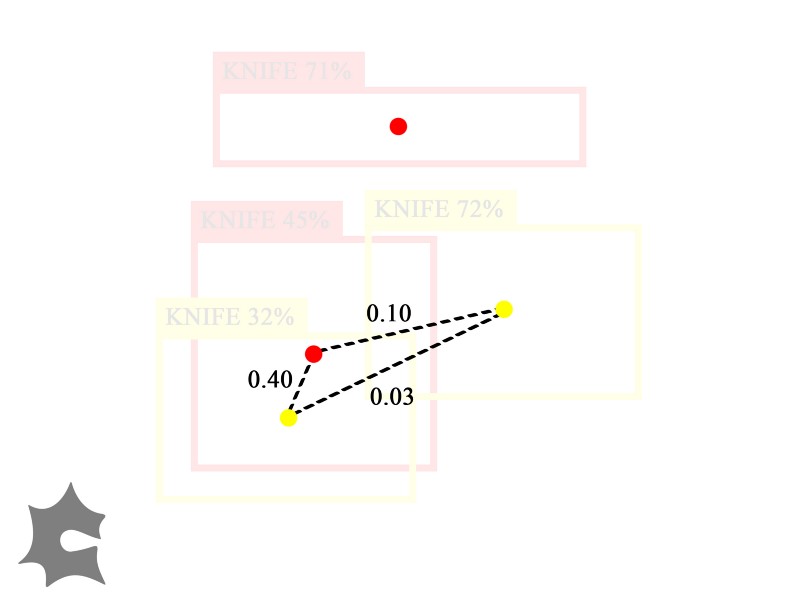A graph representation of our inferences, where weighted edges join nodes whose bounding boxes intersect.
Now we have a weighted undirected graph. Our goal is to partition each disjoint subgraph into cliques such that no two vertices in a clique share the same color. We also want the cliques to have the maximum sum of edge weights (be as overlapping as possible). We take a greedy approach to this. First, we create a clique for each vertex. Then, we sort the edges by edge weight (IoU score). In descending order of edge weight, merge the two cliques the edges would connect if their sets of vertex colors are disjoint. A pseudocode implementation of this is below.
# Create a single-element clique for each vertex
vertex_to_clique_map = {v: clique(v) for v in graph.vertices}
edges = []
for every pair of colors color1, color2:
for every pair of vertices from color1 and color2 v1, v2:
# if v1 and v2's bounding boxes overlap, they have an edge between them
if v1.bounding_box.overlap(v2.bounding_box):
edges.append(edge(v1, v2))
# sort edges by IoU score, descending
edges = sorted(edges, key=lambda edge: -edge.iou_score)
for edge in edges:
clique1 = vertex_to_clique_map[edge.v1]
clique2 = vertex_to_clique_map[edge.v2]
# if no 2 vertices in the cliques share a color, they can merge
if clique1.colors.isdisjoint(clique2.colors):
clique1.update(clique2)
vertex_to_clique_map[v2] = clique1
# return the remaining cliques
return set(vertex_to_clique_map.values())
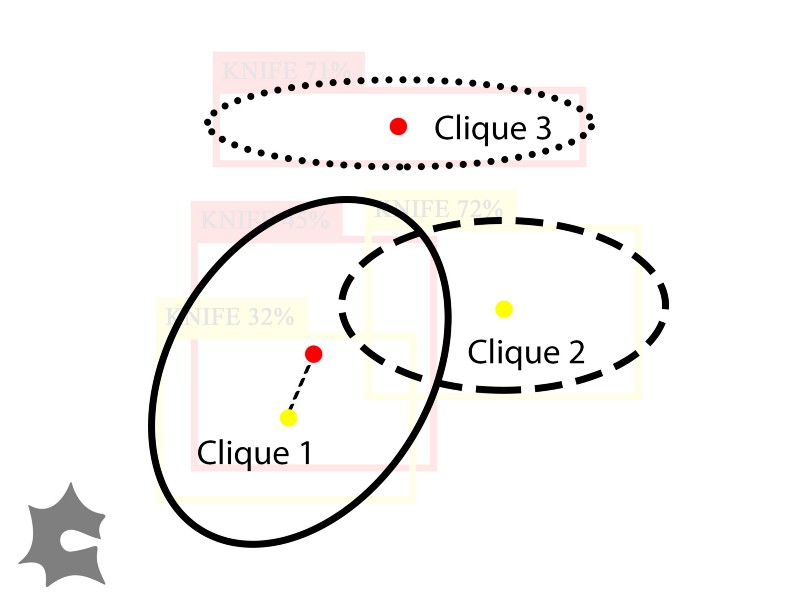We’ve grouped the detections into three cliques. The clique on the left contains two inferences.
Voting on cliques
Now we have cliques of inferences that each refer to one object in the image. Which of these cliques should we accept? The fact that only Model A detected an object near the top of the image (Clique 3) means that Model B did not think there was an object near the top of the image. Here is where we can introduce voting to increase the accuracy of our ensemble detection. A model votes for a clique if one of the inferences in the clique comes from that model, and only accept a clique if majority of voters vote for it. Let’s define a *voting threshold *as the minimum percentage of models that must vote for a clique for us to accept it.
Suppose we had a voting threshold of 0.5, so both models need to vote for a clique for us to accept it. Then we’d reject Clique 2 and Clique 3 because they each only have one vote, but we’d accept Clique 1 because it has two votes.
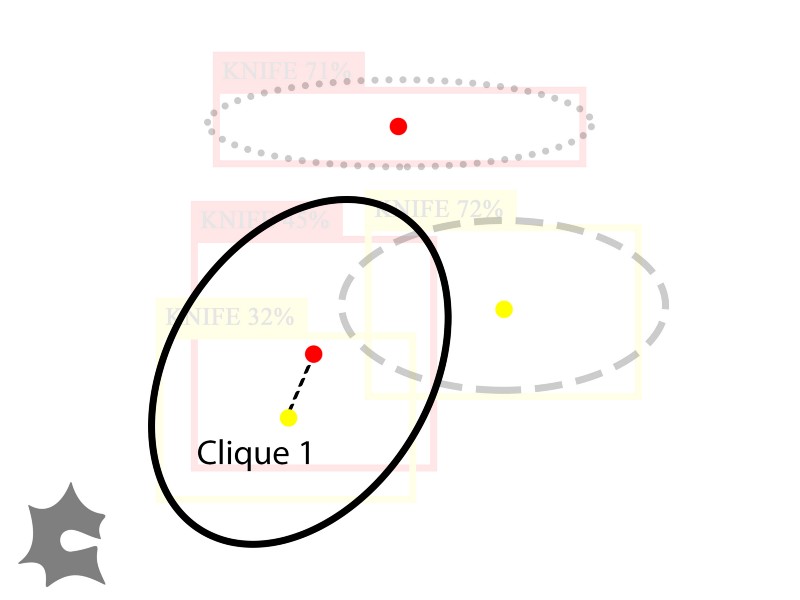Results of ensemble detection after voting: only accept Clique 1.
After voting, we only accept Clique 1. We finally compute the combined score of Clique 1 as a function of its inferences, and output a representative bounding box for this clique with that combined score as its confidence score.
Takeaways
Through effective grouping and voting schemes, multiple object detection models in ensemble can perform better than one alone. In the context of X-ray baggage screening this means more accurate detections, lower false positive rates, and ultimately a safer world.
We hope other computer vision teams can apply this technique to make more accurate and robust detection systems.
Some cool detections we’ve made at Synapse Technology, including handguns, gun parts, ammunition, razor blades, and fixed and folding knives.
I designed and implemented this system over the course of my one-month internship at Synapse Technology (acquired) this January. Thanks to my mentor Steven for thoughtful design documents and whiteboard sessions. Thanks to Sims for encouraging me to share my work, as well as the rest of the engineering team for a fun and productive internship.
Thanks to Noah Moroze, Simanta Gautam, Bruno B. Ferrari Faviero, Ian Cinnamon, and Sanjeevani Lakshmivarahan for feeback. This blog post was cross-posted on Medium here.